번외. 컴퓨터에서 음수를 표현하는 방법
컴퓨터는 0과 1의 이진수만 이해할 수 있는데, 이런 컴퓨터 세계에선 음수를 어떻게 표현할까요? 컴퓨터에서 음수를 표현하는 방법은 부호 절댓값 방식(signed magnitude), 1의 보수, 2의 보수와 같이 크게 세 가지가 있습니다. 먼저 부호 절대값 방식부터 알아보도록 하겠습니다.
부호 절댓값 방식
부호 절댓값 방식은 0과 양수, 음수를 표현할 수 있는 가장 단순한 방법입니다. 이 방식은 최상위 비트로 부호를 표현하고, 나머지 비트로 해당 정수의 절댓값을 나타냅니다. 여기서 최상위 비트(Most Significant Bit, MSB)를 부호 비트로 쓰면서 표현할 수 있는 절댓값의 범위는 절반으로 줄어들게 됩니다. 최상위 비트가 0이면 양수라는 뜻이고, 1이면 음수라는 뜻입니다.
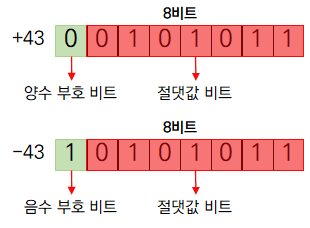
문제점
하지만 이 방식은 문제점을 가지고 있습니다. 첫 번째는 양수의 0과 음수의 0이 둘 다 존재한다는 것입니다. 컴퓨터에서 이 수가 0인지 아닌지를 확인할 때 +0인지 -0인지를 두 번이나 비교를 해야 합니다.

그리고 예를 들어서 4와 -7을 더한다고 합시다. 이를 부호 절댓값 방식으로 표현하면 각각 00000100, 10000111가 될 것입니다. 이를 일반적인 방법으로 계산하면 아래와 같이 -3이 아니라 엉뚱한 결과가 나오게 됩니다.
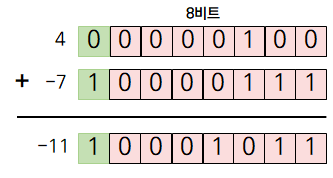
부호 절댓값 방식에선 4+(-7)은 아래와 같이 -(7-4)로 계산해야 합니다.

아래의 연산표를 보면 알 수 있듯이, 부호 절댓값 방식에서의 연산은 그렇게 간단하지 않습니다. 더욱 간단한 방법은 없을까요?

1의 보수
1의 보수는 해당 양수의 모든 비트를 반전시켜 음수를 표현하는 방법입니다. 부호 절댓값 방식과 동일하게 최상위 비트는 부호 비트로 쓰입니다.

이 방법에선 부호 절댓값 방식과는 달리 서로 다른 부호를 가진 두 수의 덧셈 연산을 보다 간단하게 해결할 수 있습니다.
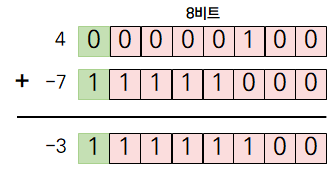
연산 시 캐리가 발생했을 때는 추가적인 연산이 필요합니다. 캐리는 최상위 비트(MSB)에서 그 위의 비트로 자리올림이 발생하는 것을 말합니다.
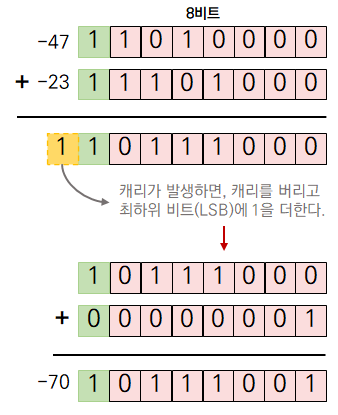
문제점
그러나 여전히 문제점이 남아 있습니다. 부호 절댓값 방식의 문제점과 동일하게, 1의 보수에도 +0, -0으로 0이 두 개가 존재합니다.
2의 보수
2의 보수는 1의 보수와 매우 비슷합니다. 2의 보수에서도 1의 보수와 동일하게 최상위 비트는 부호 비트로 쓰입니다. 어떤 수의 2의 보수를 구하려면 그 수의 1의 보수를 취한 값에 1을 더하면 됩니다.
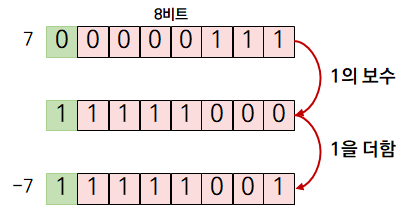
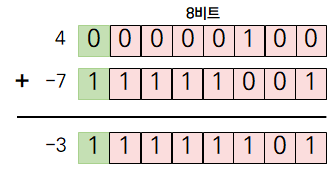
2의 보수를 이용해 4와 -7을 서로 더하면 아래와 같습니다.
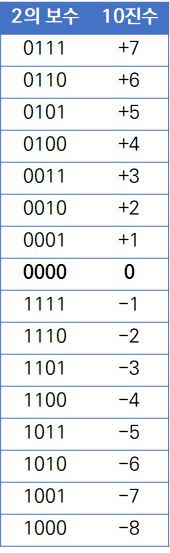
아래 표에서 확인할 수 있듯이 부호 절댓값 방식과 1의 보수에서 양의 0과 음의 0이 존재하는 문제가 해결되었음을 볼 수 있습니다.
한 걸음 더 나아가기
r진법에는 r의 보수와 r-1의 보수가 있습니다. 예를 들어서, 2진수에는 2의 보수와 1의 보수가 있고, 10진수에는 10의 보수와 9의 보수가 있습니다.
r의 보수
r진법에서 n자리의 양수 N이 주어졌을 때, N의 r의 보수는 \( N \neq 0 \)일 때 \( r^n - N \)이고, \( N = 0 \)일 때는 0이 됩니다. 예를 들어서, \( 42330_{10} \)의 10의 보수는 \( 10^5 - 42330 = 57670 \)이 되고, \( 11011_2 \)의 2의 보수는 \( (2^5)_{10} - (11011)_2 = (100000 - 11011)_2 = 00101_2 \)이 됩니다.
[작성 중]
r-1의 보수
r진법에서 n자리의 양수 N이 주어졌을 때, N의 r-1의 보수는 \( r^n - 1 - N \)이 됩니다. 예를 들어서, \( 42330_{10} \)의 9의 보수는 \( 10^5 - 1 - 42330 = 57669 \)가 되고, \( 11011_2 \)의 1의 보수는 \( (2^5 - 1) - (11011)_2 = (11111 - 11011)_2 = 00100_2 \)이 됩니다.
[작성 중]
'프로그래밍 관련 > 자바' 카테고리의 다른 글
| 정리. JVM의 힙 영역 살펴보기 (0) | 2022.01.22 |
|---|---|
| 14편. 문자열(String) (2) | 2022.01.15 |
| 번외. 10진수와 2진수 간 변환하기 (0) | 2021.08.10 |
| 자바스크립트 강좌 1편. 시작 (2) | 2016.05.09 |
| 28편. 스레드(Thread) (1) (10) | 2012.08.25 |